Bajtocka Agencja Kosmiczna正在进行一个新项目,计划在拜火星(Bajmarsie)上建造一座太空基地。项目的第一阶段已经完成:在拜火星上已经准备好了用于建造太空设施的地块。由于拜火星表面被侵蚀严重,直接在其上建造会很危险,因此在拜火星表面之上,使用金属支架搭建了矩形的平坦平台。所有平台都位于距离地表相同的高度,并且显然它们互不重叠。
现在开始基地建设的第二阶段。在已准备好的区域上将建造各种太空设施。每个设施都是长方体形状。目前已经有许多关于设施在表面上摆放位置的方案。你的任务是编写程序,对每个设施判断:是否能够将它放置在方案所指定的位置。
设施应当放在这些准备好的平台上,但其底面不必完全落在平台之上。只要设施能够在一个或多个平台上稳定站立即可。稳定站立发生在以下任一条件满足时:设施的重心位于某个平台的区域之上(边界也算在内),或者设施底面的至少三个顶点支撑在平台上。
可以假设设施的重心位于其底面两条对角线交点的正上方。若某个顶点位于平台内部或边界上,则称该顶点支撑在平台上。无需在意设施有过大部分悬空在拜火星空气中。请记住,这些只是规划方案,因此两个设施被计划建在同一位置,或不同方案之间互相冲突,都没有任何意义。
任务
编写程序,使其:
- 读入各个平台的顶点坐标以及各个设施的拟建位置;
- 对每个设施检查其是否能稳定站立;
- 对每个设施输出相应答案。
输入格式
第一行包含平台数量 $n$,$1 \le n \le 25,000$。接下来的 $n$ 行描述各个平台的位置。第 $i$ 行包含四个整数 $x_{1,i}$、$y_{1,i}$、$x_{2,i}$、$y_{2,i}$ —— 第 $i$ 个平台的左下角与右上角坐标,满足 $-10^9 \le x_{1,i} < x_{2,i} ≤ 10^9$ 且 $-10^9 \le y_{1,i} < y_{2,i} \le 10^9$。下一行包含整数 $q$ —— 设施方案数量,$1 \le q \le 25,000$。接下来的 $q$ 行每行描述一个方案。第 $j$ 行包含四个整数 $x'_{1,j}$、$y'_{1,j}$、$x'_{2,j}$、$y'_{2,j}$ —— 第 $j$ 个计划设施底面的左下角与右上角坐标,满足 $-10^9 \le x'_{1,j} < x'_{2,j} \le 10^9$ 且 $-10^9 \le y'_{1,j} < y'_{2,j} \le 10^9$。
输出格式
你的程序应输出恰好 $q$ 行。第 $j$ 行应包含一个单词 TAK,表示第 $j$ 个设施可以稳定放置;否则输出 NIE。
样例数据
输入
4 5 0 7 3 0 4 3 6 5 7 7 10 1 2 2 3 4 0 5 1 6 2 3 5 5 6 4 8 6 4 7 8 9
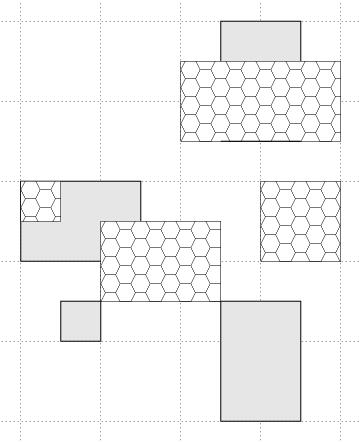
输出
TAK TAK NIE TAK