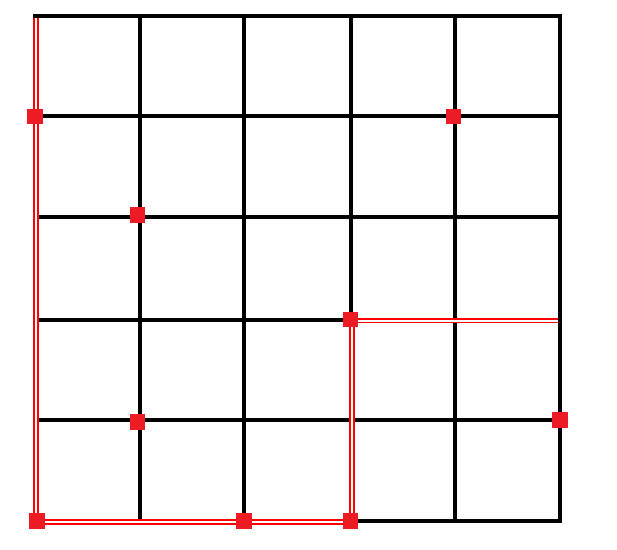
2046 年 OI 城的城市轨道交通建设终于全部竣工,由于前期规划周密,建成后的轨道交通网络由 $2n$ 条地铁线路构成,组成了一个 $n$ 纵 $n$ 横的交通网。如下图所示,这 $2n$ 条线路每条线路都包含 $n$ 个车站,而每个车站都在一组纵横线路的交汇处。
出于建设成本的考虑,并非每个车站都能够进行站内换乘,能够进行站内换乘的地铁站共有 $m$ 个,在下图中,标上方块标记的车站为换乘车站。已知地铁运行 $1$ 站需要 $2$ 分钟,而站内换乘需要步行 $1$ 分钟。 Serenade 想要知道,在不中途出站的前提下,他从学校回家最快需要多少时间(等车时间忽略不计)。
输入格式
第一行有两个整数 $n$, $m$。
接下去 $m$ 行每行两个整数 $x$, $y$,表示第 $x$ 条横向线路与第 $y$ 条纵向线路的交汇站是站内换乘站。
接下去一行是四个整数 $x_1$, $y_1$, $x_2$, $y_2$。表示 Serenade 从学校回家时,在第 $x_1$ 条横向线路与第 $y_1$ 条纵向线路的交汇站上车,在第 $x_2$ 条横向线路与第 $y_2$ 条纵向线路的交汇站下车。
输出格式
输出只有一行,即 Serenade 在合理选择线路的情况下,回家所需要的时间。如果 Serenade 无法在不出站换乘的情况下回家,请输出 -1。
样例数据
样例 1 输入
2 1 1 2 1 1 2 2
样例 1 输出
5
样例 2 输入
6 9 2 1 2 5 3 2 4 4 5 2 5 6 6 1 6 3 6 4 1 1 4 6
样例 2 输出
27
样例 3 输入
6 10 2 1 2 5 3 2 4 4 5 2 5 6 6 1 6 3 6 4 6 6 1 1 4 6
样例 3 输出
26
子任务
对于 $30\%$ 的数据,$n\le 50$, $m\le 1\,000$;
对于 $60\%$ 的数据,$n\le 500$, $m\le 2\,000$;
对于 $100\%$ 的数据,$n\le 20\,000$, $m\le 100\,000$;