You are playing a game on a number line. Your character is initially at position $s$, and there are $N$ mirrors placed on the number line. The positions of the mirrors, from left to right, are given as $A_1 \le A_2 \le \cdots \le A_N$. There may be multiple mirrors at the same position.
You can change your character’s position by using mirrors. When a mirror is used, your character moves to the point that is the reflection of its current position with respect to that mirror. That is, if your character is at position $a$ and you use a mirror located at position $b$, then your character moves to position $2b - a$.
Each of the $N$ mirrors must be used exactly once. You cannot skip any mirror, and you cannot use any mirror more than once. Aside from this restriction, you may use the mirrors in any order you like.
Under these conditions, compute and output the maximum possible final position of your character.
Constraints
All given values are integers.
- $1 \le N \le 200,000$
- $-10^9 \le s \le 10^9$
- $-10^9 \le A_1 \le A_2 \le \cdots \le A_N \le 10^9$
Scoring
- (7 points) $N \le 2$.
- (25 points) $N$ is even, $A_1 = A_2 = \cdots = A_{N/2} < s < A_{N/2+1} = A_{N/2+2} = \cdots = A_N$.
- (19 points) $N$ is even, $A_1 < s < A_N$.
- (49 points) No additional constraints.
Input Format
The first line contains two integers $N$ and $s$, the number of mirrors and your initial position.
The second line contains $N$ integers $A_1, A_2, \ldots, A_N$, representing the positions of the mirrors.
Output Format
Output the maximum possible final position of your character after using all $N$ mirrors exactly once.
Note that the answer can be large, so in some programming languages you may need to use a 64-bit integer type (such as long long).
Example
Example 1
Input
2 0 -1 2
Output
6
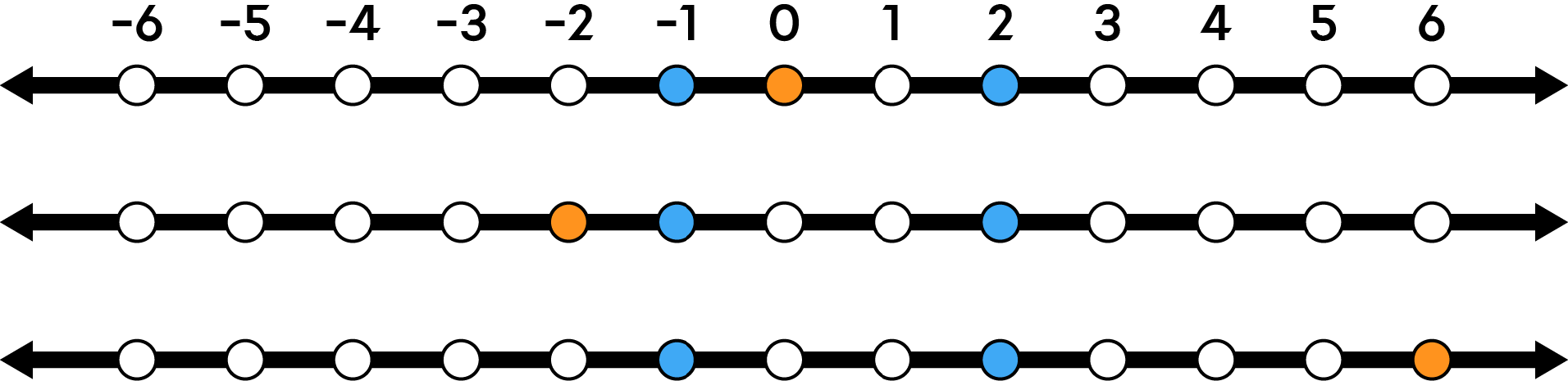
If you use mirror 1 first and then mirror 2, the final position of your character becomes $6$, as shown in the figure.
On the other hand, if you use mirror 2 first and then mirror 1, the final position becomes $-6$.
Therefore, the correct answer for this example is $6$.
Example 2
Input
6 3 -4 -2 2 6 8 9
Output
57
Example 3
Input
9 9 0 1 3 3 4 5 8 9 10
Output
49
Example 4
Input
1 1000000000 -999999999
Output
-2999999998