あなたは数直線上でゲームをしています。あなたのキャラクターは最初、位置 $s$ にいます。また、数直線上には $N$ 枚の鏡が置かれています。鏡の位置は左から右へ $A_1 \le A_2 \le \cdots \le A_N$ として与えられます。同じ位置に複数の鏡が存在することもあります。
あなたは鏡を使うことでキャラクターの位置を変えることができます。鏡を 1 枚使用すると、キャラクターはその鏡に関して現在位置の反転位置へ移動します。すなわち、キャラクターが位置 $a$ にいて、位置 $b$ にある鏡を使うと、キャラクターは位置 $2b - a$ に移動します。
$N$ 枚すべての鏡は ちょうど 1 回ずつ 使用しなければなりません。どの鏡も飛ばして使うことはできず、同じ鏡を 2 回以上使うこともできません。この制約以外には、鏡を使用する順序は自由に選ぶことができます。
以上の条件のもとで、キャラクターが最終的に到達できる 最大の位置 を求めてください。
制約
与えられる値はすべて整数である。
- $1 \le N \le 200\,000$
- $-10^9 \le s \le 10^9$
- $-10^9 \le A_1 \le A_2 \le \cdots \le A_N \le 10^9$
小課題
- (7 点)$N \le 2$。
- (25 点)$N$ は偶数であり、$A_1 = A_2 = \cdots = A_{N/2} < s < A_{N/2+1} = A_{N/2+2} = \cdots = A_N$。
- (19 点)$N$ は偶数であり、$A_1 < s < A_N$。
- (49 点)追加の制約なし。
入力
1 行目に整数 $N$ と $s$ が与えられる。これは鏡の枚数と初期位置を表す。
2 行目に $N$ 個の整数 $A_1, A_2, \ldots, A_N$ が与えられ、鏡の位置を表す。
出力
すべての鏡をちょうど 1 回ずつ使用した後の、キャラクターの最終位置として考えられる最大値を出力せよ。
答えは非常に大きくなる可能性があるため、使用するプログラミング言語によっては 64 ビット整数型(例:long long)を用いる必要があることに注意せよ。
例
例 1
入力
2 0 -1 2
出力
6
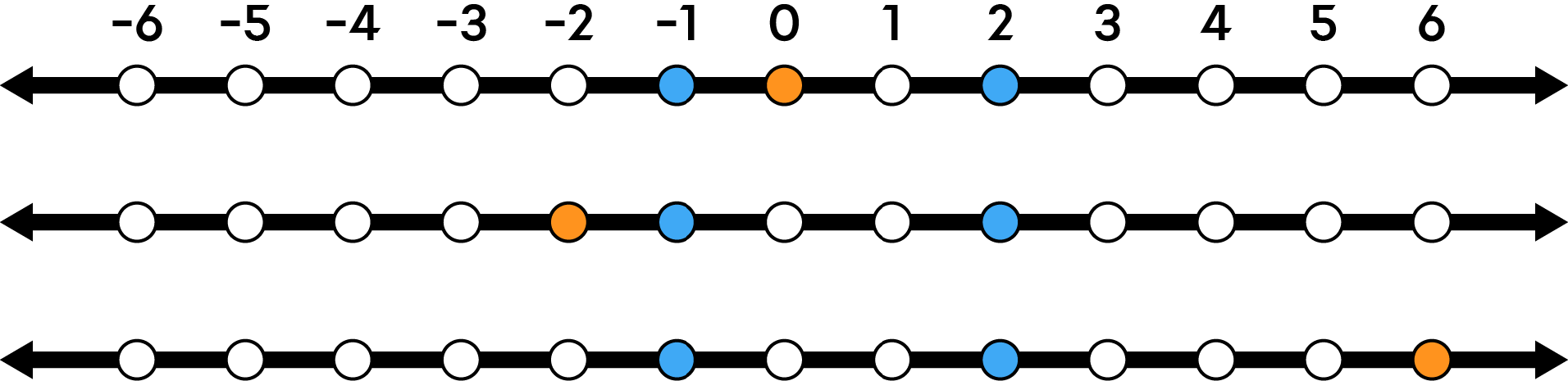
まず鏡 1 を使用し、その後に鏡 2 を使用すると、図のようにキャラクターの最終位置は $6$ になります。
一方で、先に鏡 2 を使用し、その後に鏡 1 を使用すると、最終位置は $-6$ になります。
したがって、この例の正しい答えは $6$ です。
例 2
入力
6 3 -4 -2 2 6 8 9
出力
57
例 3
入力
9 9 0 1 3 3 4 5 8 9 10
出力
49
例 4
入力
1 1000000000 -999999999
出力
-2999999998