你正在数轴上玩一个游戏。你的角色初始位于位置 $s$,数轴上放置了 $N$ 面镜子。镜子从左到右的位置为 $A_1 \le A_2 \le \cdots \le A_N$。可能有多面镜子位于同一位置。
你可以通过使用镜子来改变角色的位置。使用一面镜子时,你的角色会移动到相对于该镜子的当前位置的对称点。也就是说,如果你的角色在位置 $a$,使用位于位置 $b$ 的镜子,那么你的角色会移动到位置 $2b-a$。
这 $N$ 面镜子都必须恰好使用一次。你不能跳过任何镜子,也不能重复使用同一面镜子。除此限制外,你可以按任意顺序使用镜子。
在这些条件下,计算并输出你的角色最终位置的最大可能值。
限制
所有给定值均为整数。
- $1 \le N \le 200,000$
- $-10^9 \le s \le 10^9$
- $-10^9 \le A_1 \le A_2 \le \cdots \le A_N \le 10^9$
子任务
- (7 分)$N \le 2$。
- (25 分)$N$ 为偶数,$A_1 = A_2 = \cdots = A_{N/2} < s < A_{N/2+1} = A_{N/2+2} = \cdots = A_N$。
- (19 分)$N$ 为偶数,$A_1 < s < A_N$。
- (49 分)无额外限制。
输入格式
第一行包含两个整数 $N$ 和 $s$,分别表示镜子的数量以及你的初始位置。
第二行包含 $N$ 个整数 $A_1, A_2, \ldots, A_N$,表示镜子的位置。
输出格式
输出在恰好使用完全部 $N$ 面镜子一次之后,你的角色最终位置的最大可能值。
注意答案可能很大,因此在某些编程语言中你可能需要使用 64 位整数类型(例如 long long)。
样例数据
样例数据 1
输入
2 0 -1 2
输出
6
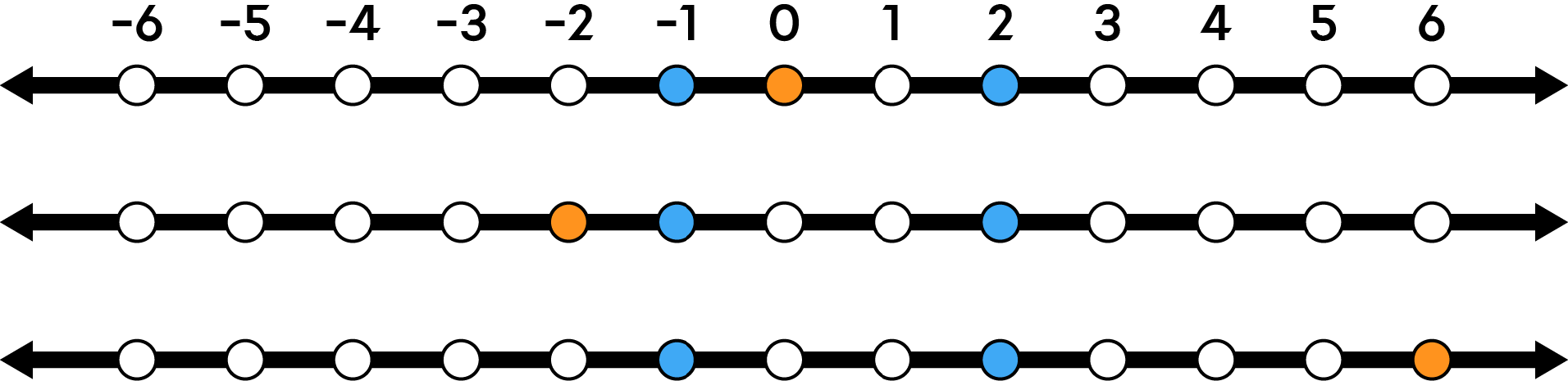
如果先使用镜子 1 再使用镜子 2,如图所示,你的角色最终位置会变为 $6$。
另一方面,如果先使用镜子 2 再使用镜子 1,最终位置会变为 $-6$。
因此,该样例的正确答案是 $6$。
样例数据 2
输入
6 3 -4 -2 2 6 8 9
输出
57
样例数据 3
输入
9 9 0 1 3 3 4 5 8 9 10
输出
49
样例数据 4
输入
1 1000000000 -999999999
输出
-2999999998