Jungol is trying to store boxes in a warehouse. There are a total of $N$ boxes, numbered from $1$ to $N$. For box $i$ $(1 \le i \le N)$, its size is $s_i$ and its storage capacity is $c_i$. For all boxes, the storage capacity is smaller than the size, that is, $c_i < s_i$.
Thinking that the warehouse is too cluttered with many boxes, Jungol wants to store boxes by putting them inside other boxes. At this time, the following conditions must be satisfied.
- A box can contain another box whose size is less than or equal to its storage capacity.
- It is also allowed to put a box that already contains another box into a different box.
- Each box can directly contain at most one other box. In other words, a box may contain at most one box directly, but that contained box may itself contain other boxes.
The cost of storing boxes is defined as the number of boxes that are not contained in any other box.
For example, suppose $N = 4$, and the sizes and storage capacities of the four boxes are as shown in the table below.
| Number | Size | Storage Capacity |
|---|---|---|
| 1 | 6 | 4 |
| 2 | 5 | 1 |
| 3 | 9 | 8 |
| 4 | 2 | 1 |
If box 4 is put into box 1, and box 1 is put into box 3 as illustrated, then the number of boxes not contained in any other box is 2, so the storage cost is 2.

However, if box 2 and box 4 are both put into box 3 as illustrated, then box 3 directly contains two boxes, so the conditions are not satisfied.
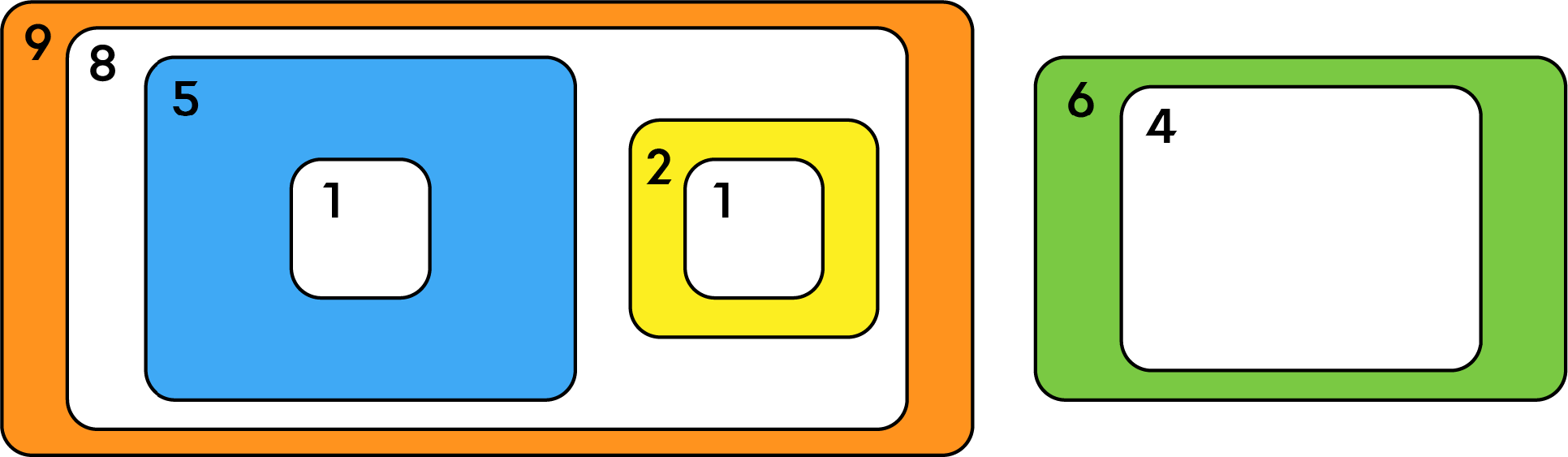
Help Jungol by writing a program that, for every $i$ from $1$ to $N$, computes the minimum cost required to store boxes $1, 2, \ldots, i$.
Constraints
- All given values are integers.
- $2 \le N \le 2 \times 10^5$
- $1 \le c_i < s_i \le 10^9 \quad (1 \le i \le N)$
Scoring
- (7 points) $N \le 6$.
- (12 points) $s_i = c_i + 1$.
- (26 points) $N \le 1000$.
- (17 points) $s_i \le 100$.
- (38 points) No additional constraints.
Input Format
The first line contains the number of boxes $N$. From the second line, $N$ lines follow, each describing a box. In the $i$-th of these lines, the size $s_i$ and the storage capacity $c_i$ of box $i$ are given, separated by a space.
Output Format
Print $N$ lines. On the $i$-th line $(1 \le i \le N)$, output the minimum cost required to store boxes $1, 2, \ldots, i$.
Example
Example 1
Input
4 6 4 5 1 9 8 2 1
Output
1 2 2 2
Example 2
Input
6 3 2 5 4 3 2 4 3 4 3 3 2
Output
1 1 2 2 2 3
Example 3
Input
8 1 3 6 7 5 9 4 1 1 0 4 2 1 5 5 1
Output
1 2 3 3 3 4 4 5