Jungol 正在尝试把箱子存放在仓库里。共有 $N$ 个箱子,编号从 $1$ 到 $N$。
对于箱子 $i$($1 \le i \le N$),其大小为 $s_i$,可容纳容量为 $c_i$。对所有箱子都有 $c_i < s_i$(即容量小于大小)。
Jungol 觉得仓库里箱子太多太乱,想通过把箱子放进其他箱子里来存放。此时必须满足以下条件。
- 一个箱子可以容纳另一个箱子,当且仅当被放入箱子的大小小于等于外箱的可容纳容量。
- 允许把一个已经包含了其他箱子的箱子,再放入另一个箱子中。
- 每个箱子最多只能直接包含一个其他箱子。换句话说,一个箱子最多直接包含一个箱子,但那个被包含的箱子本身可以继续包含其他箱子。
存放箱子的费用定义为:不被任何其他箱子包含的箱子数量。
例如,设 $N = 4$,四个箱子的大小与可容纳容量如下表所示。
| 编号 | 大小 | 可容纳容量 |
|---|---|---|
| 1 | 6 | 4 |
| 2 | 5 | 1 |
| 3 | 9 | 8 |
| 4 | 2 | 1 |
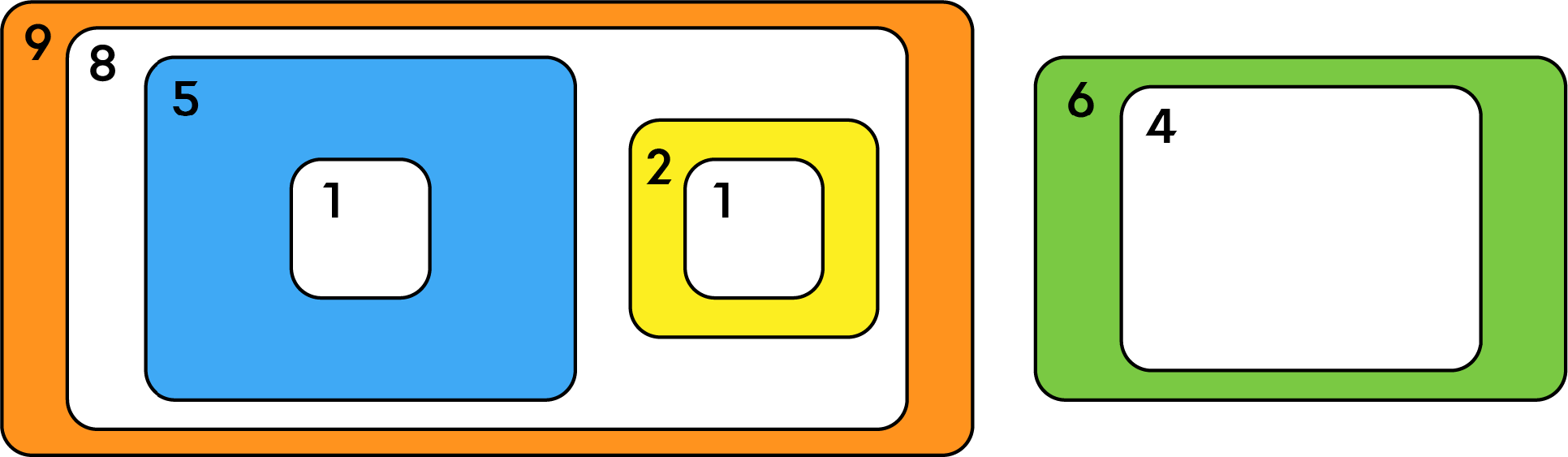
若将箱子 4 放入箱子 1,再将箱子 1 放入箱子 3,如图所示,则不被任何其他箱子包含的箱子数量为 2,所以存放费用为 2。

然而,若如图所示将箱子 2 和箱子 4 都放入箱子 3,则箱子 3 直接包含了两个箱子,违反条件。
Jungol 并不一定要把所有箱子都保留在仓库里,计划只存放编号较小的一部分箱子,丢弃其余箱子。Jungol 还没有决定要使用多少个箱子。
请你帮助 Jungol:对于每个 $i$(从 $1$ 到 $N$),计算存放箱子 $1,2,\ldots,i$ 所需的最小费用。
限制
- 所有给定值均为整数。
- $2 \le N \le 2 \times 10^5$
- $1 \le c_i < s_i \le 10^9 \quad (1 \le i \le N)$
子任务
1.(7 分)$N \le 6$。 2.(12 分)$s_i = c_i + 1$。 3.(26 分)$N \le 1000$。 4.(17 分)$s_i \le 100$。 5.(38 分)无额外限制。
输入格式
第一行给出箱子数量 $N$。 从第二行开始,共有 $N$ 行,每行描述一个箱子。 第 $i$ 行给出箱子 $i$ 的大小 $s_i$ 与可容纳容量 $c_i$,用空格分隔。
输出格式
输出 $N$ 行。 第 $i$ 行($1 \le i \le N$)输出存放箱子 $1,2,\ldots,i$ 所需的最小费用。
样例数据
样例数据 1
输入
4 6 4 5 1 9 8 2 1
输出
1 2 2 2
样例数据 2
输入
6 3 2 5 4 3 2 4 3 4 3 3 2
输出
1 1 2 2 2 3
样例数据 3
输入
8 1 3 6 7 5 9 4 1 1 0 4 2 1 5 5 1
输出
1 2 3 3 3 4 4 5