For an integer $N \ge 2$, consider a situation where $N$ vertices labeled from $1$ to $N$ are placed in a straight line in increasing order of their labels. For each $i$ $(1 \le i \le N-1)$, there is an undirected edge connecting vertex $i$ and vertex $i+1$.

For example, when $N = 5$, the vertices and edges are arranged as shown in the figure.

Jeongol can move on this graph by jumping. When Jeongol jumps from one vertex to another vertex, he traverses every edge between them exactly once.

For example:

• If Jeongol jumps from vertex $4$ to vertex $2$, he traverses the edge between vertices $3$ and $4$, and the edge between vertices $2$ and $3$, once each.
• If Jeongol jumps from vertex $3$ to vertex $4$, he traverses the edge between vertices $3$ and $4$ once.

Jeongol starts at vertex $1$, makes exactly $N-1$ jumps, and arrives at vertex $N$. During this process, he visits every vertex exactly once. (Being at vertex $1$ initially is also considered a visit.)

In other words, if the order in which Jeongol visits the vertices is $p_1 \to p_2 \to \cdots \to p_{N-1} \to p_N$, then $p_1 = 1$, $p_N = N$, and ${p_1, p_2, \ldots, p_N} = {1, 2, \ldots, N}$.

For each $i$ $(1 \le i \le N-1)$, let $c_i$ be the number of times the edge between vertex $i$ and vertex $i+1$ is traversed during Jeongol’s jumps.

For example, if Jeongol visits the vertices in the order $(p_1 = 1) \to (p_2 = 3) \to (p_3 = 4) \to (p_4 = 2) \to (p_5 = 5)$, then $c_1 = 1$, $c_2 = 3$, $c_3 = 3$, $c_4 = 1$.

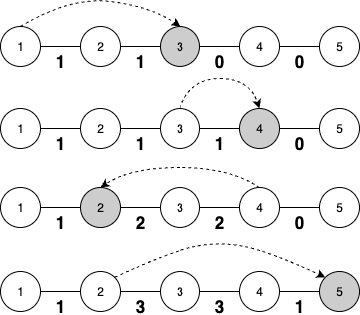
You are given the sequence $c = (c_1, c_2, \ldots, c_{N-1})$, which represents how many times each edge was traversed. From this, write a program to determine a possible visiting order $p_1, p_2, \ldots, p_N$ of Jeongol.

The given sequence $c$ is always generated by some valid visiting order, so at least one solution always exists. If there are multiple possible visiting orders, output any one of them.

Constraints

• All given values are integers.
• $2 \le N \le 200,000$
• For all $i$ $(1 \le i \le N-1)$, $1 \le c_i \le 10^9$
• The input always guarantees that at least one valid visiting order exists.

Scoring

1. (10 points) $N \le 10$.
2. (10 points) For all $i$ $(1 \le i \le N-1)$, $c_i \le 3$.
3. (15 points) $N \ge 4$, and there exists an integer $M$ with $2 \le M \le N-2$ such that $c_1 \le c_2 \le \cdots \le c_M$ and $c_M \ge c_{M+1} \ge \cdots \ge c_{N-1}$. That is, the sequence $c$ first increases monotonically and then decreases monotonically.
4. (35 points) $N \le 300$.
5. (30 points) No additional constraints.

Input

The first line contains an integer $N$, the number of vertices.

The second line contains $N-1$ integers $c_1, c_2, \ldots, c_{N-1}$ separated by spaces. Here, $c_i$ denotes the number of times the edge between vertex $i$ and vertex $i+1$ is traversed.

Output

Output a possible visiting order $p_1, p_2, \ldots, p_N$ separated by spaces. If there are multiple valid visiting orders, output any one of them.

Example

Example 1

Input

5
1 3 3 1

Output

1 3 4 2 5

Example 2

Input

7
1 3 3 5 3 1

Output

1 6 2 3 5 4 7