整数 $N \ge 2$ に対して、$1$ から $N$ までの番号が付いた $N$ 個の頂点が、番号の昇順に一直線上に配置されている状況を考える。各 $i$ $(1 \le i \le N-1)$ について、頂点 $i$ と頂点 $i+1$ を結ぶ無向辺が存在する。
例えば、$N = 5$ のとき、頂点と辺の配置は次の図のようになる。

Jeongol はこのグラフ上をジャンプによって移動することができる。Jeongol がある頂点から別の頂点へジャンプするとき、その間に存在するすべての辺をちょうど一度ずつ通過する。
例えば:
- Jeongol が頂点 $4$ から頂点 $2$ へジャンプすると、頂点 $3$ と $4$ の間の辺、および頂点 $2$ と $3$ の間の辺を、それぞれ一度ずつ通過する。
- Jeongol が頂点 $3$ から頂点 $4$ へジャンプすると、頂点 $3$ と $4$ の間の辺を一度通過する。
Jeongol は頂点 $1$ から出発し、ちょうど $N-1$ 回のジャンプを行って、頂点 $N$ に到達する。この過程で、すべての頂点をちょうど一度ずつ訪れる(初期状態で頂点 $1$ にいることも訪問として数える)。
言い換えると、Jeongol が頂点を訪れる順序を $p_1 \to p_2 \to \cdots \to p_{N-1} \to p_N$ とすると、$p_1 = 1$、$p_N = N$、かつ ${p_1, p_2, \ldots, p_N} = {1, 2, \ldots, N}$ が成り立つ。
各 $i$ $(1 \le i \le N-1)$ について、$c_i$ を、Jeongol のジャンプ中に頂点 $i$ と頂点 $i+1$ の間の辺が通過される回数とする。
例えば、Jeongol が $(p_1 = 1) \to (p_2 = 3) \to (p_3 = 4) \to (p_4 = 2) \to (p_5 = 5)$ の順に頂点を訪れた場合、 $c_1 = 1$、$c_2 = 3$、$c_3 = 3$、$c_4 = 1$ となる。
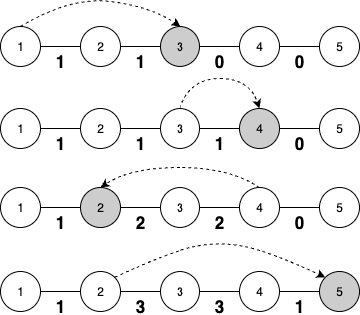
各辺が何回通過されたかを表す数列 $c = (c_1, c_2, \ldots, c_{N-1})$ が与えられる。これに基づいて、Jeongol の訪問順序 $p_1, p_2, \ldots, p_N$ の一例を求めるプログラムを書きなさい。
与えられる数列 $c$ は、必ず何らかの有効な訪問順序から生成されたものであるため、少なくとも一つの解は常に存在する。複数の訪問順序が可能な場合は、そのうちの任意の一つを出力してよい。
制約
- 入力される値はすべて整数である。
- $2 \le N \le 200{,}000$
- すべての $i$ $(1 \le i \le N-1)$ について、$1 \le c_i \le 10^9$
- 入力は、少なくとも一つの有効な訪問順序が存在することを保証する。
小課題
- (10 点) $N \le 10$。
- (10 点) すべての $i$ $(1 \le i \le N-1)$ について、$c_i \le 3$。
- (15 点) $N \ge 4$ であり、$2 \le M \le N-2$ を満たす整数 $M$ が存在して、 $c_1 \le c_2 \le \cdots \le c_M$ かつ $c_M \ge c_{M+1} \ge \cdots \ge c_{N-1}$ が成り立つ。 すなわち、数列 $c$ は最初単調増加し、その後単調減少する。
- (35 点) $N \le 300$。
- (30 点) 追加の制約なし。
入力
1 行目に、頂点の数を表す整数 $N$ が与えられる。
2 行目に、$N-1$ 個の整数 $c_1, c_2, \ldots, c_{N-1}$ が空白区切りで与えられる。ここで、$c_i$ は頂点 $i$ と頂点 $i+1$ の間の辺が通過された回数を表す。
出力
Jeongol の訪問順序 $p_1, p_2, \ldots, p_N$ を空白区切りで出力せよ。複数の有効な訪問順序が存在する場合は、そのうちの任意の一つを出力してよい。
例
例 1
入力
5 1 3 3 1
出力
1 3 4 2 5
例 2
入力
7 1 3 3 5 3 1
出力
1 6 2 3 5 4 7