跳跃 - 問題

对于整数 $N \ge 2$，将 $N$ 个顶点按编号从 $1$ 到 $N$ 依次放在一条直线上。对每个 $i$（$1 \le i \le N-1$），存在一条连接顶点 $i$ 与顶点 $i+1$ 的无向边。

例如，当 $N = 5$ 时，顶点与边的排列如下图所示。

Jeongol 可以通过跳跃在该图上移动。当 Jeongol 从一个顶点跳到另一个顶点时，他会将它们之间的每一条边恰好经过一次。

例如：

Jeongol 从顶点 $1$ 出发，恰好进行 $N-1$ 次跳跃，并到达顶点 $N$。在此过程中，他恰好访问每个顶点一次。（初始时位于顶点 $1$ 也视为一次访问。）

换句话说，若 Jeongol 访问顶点的顺序为 $p_1 \to p_2 \to \cdots \to p_{N-1} \to p_N$，则 $p_1 = 1$，$p_N = N$，且 ${p_1, p_2, \ldots, p_N} = {1, 2, \ldots, N}$。

对每个 $i$（$1 \le i \le N-1$），设 $c_i$ 表示在 Jeongol 的跳跃过程中，顶点 $i$ 与顶点 $i+1$ 之间的边被经过的次数。

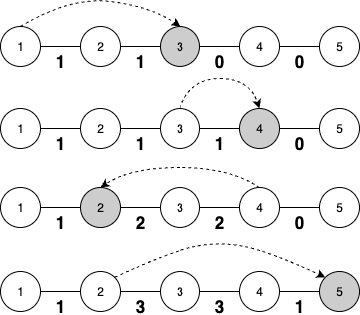
例如，若 Jeongol 访问顶点的顺序为 $(p_1 = 1) \to (p_2 = 3) \to (p_3 = 4) \to (p_4 = 2) \to (p_5 = 5)$，则 $c_1 = 1$，$c_2 = 3$，$c_3 = 3$，$c_4 = 1$。

给定序列 $c = (c_1, c_2, \ldots, c_{N-1})$，表示每条边被经过的次数。请你编写程序，求出一种可能的访问顺序 $p_1, p_2, \ldots, p_N$。

给定的序列 $c$ 一定由某个合法的访问顺序生成，因此至少存在一个解。若存在多个可能的访问顺序，输出任意一个即可。

（10 分）$N \le 10$。
（10 分）对所有 $i$（$1 \le i \le N-1$），$c_i \le 3$。
（15 分）$N \ge 4$，且存在整数 $M$ 满足 $2 \le M \le N-2$，使得 $c_1 \le c_2 \le \cdots \le c_M$ 且 $c_M \ge c_{M+1} \ge \cdots \ge c_{N-1}$。即序列 $c$ 先单调不减后单调不增。
（35 分）$N \le 300$。
（30 分）无额外限制。

第一行包含一个整数 $N$，表示顶点个数。

第二行包含 $N-1$ 个整数 $c_1, c_2, \ldots, c_{N-1}$，用空格分隔。其中 $c_i$ 表示顶点 $i$ 与顶点 $i+1$ 之间的边被经过的次数。

输出一个可能的访问顺序 $p_1, p_2, \ldots, p_N$，用空格分隔。若有多个合法答案，输出任意一个即可。

输入

5
1 3 3 1

输出

1 3 4 2 5

输入

7
1 3 3 5 3 1

输出

1 6 2 3 5 4 7

QOJ.ac